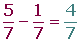OPERACIONES CON NÚMEROS RACIONALES

Suma y resta de números racionales

Con el mismo denominador

Se suman o se restan los numeradores y se mantiene el denominador.

              

EJEMPLOS.

              

Con distinto denominador

En primer lugar se reducen los denominadores a común denominador, y se suman o se restan los numeradores de las fracciones equivalentes obtenidas.

              

EJEMPLOS.

          

APLICACIONES EN LA VIDA REAL

ESTUDIANTES DE LA UNIDAD EDUCATIVA "REPÚBLICA DE CANADÁ" EXPONIENDO SITUACIONES REALES EN LAS QUE SE PRESENTAN LOS NÚMEROS RACIONALES 

                    

URL PARA CONSULTAR: 

- https://www.youtube.com/watch?v=9kPI78Kg288

- https://www.youtube.com/watch?v=RHbAyf8SPGs

REPRESENTACIÓN GRÁFICA DE LOS NÚMEROS RACIONALES

Los números racionales se representan en la recta numérica junto a los números enteros.

Para representar con precisión los números racionales:

1. Tomamos un segmento de longitud la unidad, por ejemplo.

2. Trazamos un segmento auxiliar desde el origen y lo dividimos en las partes que deseemos. En nuestro ejemplo, lo dividimos en 4 partes.

3. Unimos el último punto del segmento auxiliar con el extremo del otro segmento y trazamos segmentos paralelos en cada uno de los puntos, obtenidos en la partición del segmento auxiliar.

En la práctica se utilizan número racional y fracción como sinónimos.

NÚMEROS RACIONALES EN LA VIDA COTIDIANA

Los números racionales, son el conjunto de números fraccionarios y números enteros representados por medio de fracciones. Este conjunto está situado en la recta real numérica pero a diferencia de los números reales que son consecutivos, por ejemplo a 4 le sigue 5 y a este a su vez le sigue el 6, y los números negativos cuya consecución se da así, a -9 le sigue -8 y a este a su vez le sigue -7; los números racionales no poseen consecución pues entre cada número racional existen infinitos números que solo podrían ser escritos durante toda la eternidad.

Todos los números fraccionarios son números racionales y sirven para representar medidas. Pero a veces es más conveniente expresar un número de esta manera que convertirlo a decimal exacto o periódico, debido a la gran cantidad de decimales que se podrían obtener.

Un número racional es todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por Q.

Propiedades de los números racionales

Propiedad interna:

Es la que al sumar dos números racionales el resultado siempre será otro número racional, aunque este resultado puede ser reducido a su mínima expresión si el caso lo necesitara.

Propiedad asociativa:

Se dice que si se agrupan los diferentes sumandos racionales, el resultado no cambia y seguirá siendo un número racional. 

Propiedad conmutativa:

Es la operación donde, si el orden de los sumandos varía, el resultado no cambia.

Elemento neutro:

El elemento neutro es una cifra nula la cual si es sumada a cualquier número racional, la respuesta será el mismo número racional.

Elemento opuesto ó numero opuesto:

Es la propiedad de números racionales según la cual existe un elemento negativo que anula la existencia del otro. Es decir, que al sumarlos se obtiene como resultado el cero.

UTILIDAD DE LOS NÚMEROS RACIONALES

Los números racionales debido a que están conformados por todos los enteros y fraccionarios y a su ves estos incluyen a los Números enteros y fraccionarios consideramos a todos ellos utilizados en nuestra vida cotidiana.

Por ejemplo:

Los números acotan todo lo que nos rodea, con pruebas sencillas podemos experimentar la aplicación de la aritmética en la vida cotidiana, desde los sistemas decimales para medir la distancia y la temperatura hasta la utilización del comercio electrónico y el cálculo del número de asistentes a una manifestación.

Empezamos por lo más sencillo: ¿Cómo saber cuántas ovejas tenemos?, o ¿Cuántas se comió el lobo? hay que contar y para ello utilizamos los números naturales: 1,2,3,4,5...

¿Qué día es hoy?, ¿Cuándo naciste?, hay que contar y ordenar y para ello usamos los números cardinales: 0,1,2,3.....

¿Cómo representar las temperaturas bajo cero? ¿Cómo contar cuando debemos más de lo que tenemos? Hay que contar a ambos lados de una referencia, y para ello usamos los números enteros:: -3, -2, -1, 0, 1... 

¿Cómo repartir un premio entre tres? ¿Cómo medir con la exactitud deseada? Hay que repartir y comparar, para lo que hay que usa los números racionales: ½, 2/3, ¼... 
Pero podemos complicarlo todavía más: algo tan cotidiano y sencillo como una tarjeta de crédito contiene una clave cifrada en una fórmula matemática, conocida como proporción áurea, que ha seducido a los artistas desde la Antigüedad, y que explica desde la belleza del templo del Partenón, en Atenas, y la del hombre de Vitrubio de Leonardo hasta la de los elegantes mecheros Dupont.

Y encontramos más ejemplos: los automóviles registran el trayecto recorrido aplicando el número Pi (la razón entre el perímetro de la circunferencia y el diámetro) al giro de las ruedas; las hojas de papel DIN A 4 se miden a partir de una raíz cuadrada y las ramificaciones del sistema nervioso se pueden comprender con un tipo de número llamado fractal.

Pi, hallado hacia 1650 a.C., del que se han encontrado 4.294 millones de decimales (según la Universidad de Tokio), es uno de los números estrella del "salón de la fama de las cifras", que enmarca la muestra. Otros son el Gúgol, una cantidad mareante que consiste en un 1 seguido de cien ceros, algo más que la cantidad de partículas elementales que hay en todo el universo (10 elevado a 80). O el 9 elevado a 9 elevado a 9, que es el mayor número con notación decimal que puede escribirse con tres dígitos. Su resultado es un mastodonte de 369.693.100 dígitos. 

Es así que a diario venimos usando desde que tenemos uso de razón los números y en especial los Racionales.